LC 1786. 从第一个节点出发到最后一个节点的受限路径数
题目描述
这是 LeetCode 上的 1786. 从第一个节点出发到最后一个节点的受限路径数 ,难度为 中等。
现有一个加权无向连通图。
给你一个正整数 n ,表示图中有 n 个节点,并按从 1 到 n 给节点编号。
另给你一个数组 edges,其中每个 $edges[i] = [u{i}, v{i}, weight{i}]$ 表示存在一条位于节点 $u{i}$ 和 $v{i}$ 之间的边,这条边的权重为 $weight{i}$ 。
从节点 start 出发到节点 end 的路径是一个形如 $[z{0}, z{1}, z{2}, …, z{k}]$ 的节点序列,满足 $z{0} = start$ 、$z{k} = end$ 且在所有符合 $0 <= i <= k-1$ 的节点 $z{i}$ 和 $z{i}+1$ 之间存在一条边。
路径的距离定义为这条路径上所有边的权重总和。用 distanceToLastNode(x) 表示节点 n 和 x 之间路径的最短距离。
受限路径为满足 $distanceToLastNode(z{i}) > distanceToLastNode(z{i}+1)$ 的一条路径,其中 $0 <= i <= k-1$ 。
返回从节点 1 出发到节点 n 的 受限路径数 。
由于数字可能很大,请返回对 $10^9 + 7$ 取余的结果。
示例 1:
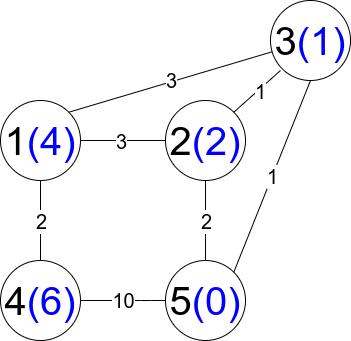
1 | |
示例 2:
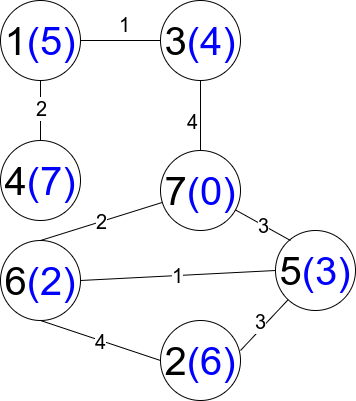
1 | |
提示:
- $1 <= n <= 2 \times 10^4$
- $n - 1 <= edges.length <= 4 \times 10^4$
- $edges[i].length = 3$
- $1 <= ui, vi <= n$
- $u_i != v_i$
- $1 <= weighti <= 10^5$
- 任意两个节点之间至多存在一条边
- 任意两个节点之间至少存在一条路径
堆优化 Dijkstra + 动态规划
n 为点的数量,m 为边的数量。
为了方便理解,我们将第 n 个点称为「起点」,第 1 个点称为「结尾」。
按照题意,我们需要先求每个点到结尾的「最短路」,求最短路的算法有很多,通常根据「有无负权边」& 「稠密图还是稀疏图」进行选择。
该题只有正权变,而且“边”和“点”的数量在一个数量级上,属于稀疏图。
因此我们可以采用「最短路」算法:堆优化的 Dijkstra,复杂度为 $O(m\log{n})$。
PS. 通常会优先选择 SPFA,SPFA 通常情况下复杂度为 $O(m)$,但最坏情况下复杂度为 $O(n \times m)$。从数据上来说 SPFA 也会超,而且本题还结合了 DP,因此可能会卡掉图论部分的 SPFA。出于这些考虑,我直接使用堆优化 Dijkstra。
当我们求得了每个点到结尾的「最短路」之后,接下来我们需要求得从「起点」到「结尾」的受限路径数量。
这显然可以用 DP 来做。
我们定义 f(i) 为从第 i 个点到结尾的受限路径数量,f(1) 就是我们的答案,而 f(n) = 1 是一个显而易见的起始条件。
因为题目的受限路径数的定义,我们需要找的路径所包含的点,必须是其距离结尾的最短路越来越近的。
举个🌰,对于示例 1,其中一条符合要求的路径为 1 --> 2 --> 3 --> 5。
这条路径的搜索过程可以看做,从结尾(第 5 个点)出发,逆着走,每次选择一个点(例如 a)之后,再选择下一个点(例如 b)时就必须满足最短路距离比上一个点(点 a)要远,如果最终能选到起点(第一个点),说明统计出一条有效路径。
我们的搜索方式决定了需要先按照最短路距离进行从小到大排序。
不失一般性,当我们要求 f(i) 的时候,其实找的是 i 点可以到达的点 j,并且 j 点到结尾的最短路要严格小于 i 点到结尾的最短路。
符合条件的点 j 有很多个,将所有的 f(j) 累加即是 f(i)。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60class Solution {
int mod = 1000000007;
public int countRestrictedPaths(int n, int[][] es) {
// 预处理所有的边权。 a b w -> a : { b : w } + b : { a : w }
Map<Integer, Map<Integer, Integer>> map = new HashMap<>();
for (int[] e : es) {
int a = e[0], b = e[1], w = e[2];
Map<Integer, Integer> am = map.getOrDefault(a, new HashMap<Integer, Integer>());
am.put(b, w);
map.put(a, am);
Map<Integer, Integer> bm = map.getOrDefault(b, new HashMap<Integer, Integer>());
bm.put(a, w);
map.put(b, bm);
}
// 堆优化 Dijkstra:求 每个点 到 第n个点 的最短路
int[] dist = new int[n + 1];
boolean[] st = new boolean[n + 1];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[n] = 0;
Queue<int[]> q = new PriorityQueue<int[]>((a, b)->a[1]-b[1]); // 点编号,点距离。根据点距离从小到大
q.add(new int[]{n, 0});
while (!q.isEmpty()) {
int[] e = q.poll();
int idx = e[0], cur = e[1];
if (st[idx]) continue;
st[idx] = true;
Map<Integer, Integer> mm = map.get(idx);
if (mm == null) continue;
for (int i : mm.keySet()) {
dist[i] = Math.min(dist[i], dist[idx] + mm.get(i));
q.add(new int[]{i, dist[i]});
}
}
// dp 过程
int[][] arr = new int[n][2];
for (int i = 0; i < n; i++) arr[i] = new int[]{i + 1, dist[i + 1]}; // 点编号,点距离
Arrays.sort(arr, (a, b)->a[1]-b[1]); // 根据点距离从小到大排序
// 定义 f(i) 为从第 i 个点到结尾的受限路径数量
// 从 f[n] 递推到 f[1]
int[] f = new int[n + 1];
f[n] = 1;
for (int i = 0; i < n; i++) {
int idx = arr[i][0], cur = arr[i][1];
Map<Integer, Integer> mm = map.get(idx);
if (mm == null) continue;
for (int next : mm.keySet()) {
if (cur > dist[next]) {
f[idx] += f[next];
f[idx] %= mod;
}
}
// 第 1 个节点不一定是距离第 n 个节点最远的点,但我们只需要 f[1],可以直接跳出循环
if (idx == 1) break;
}
return f[1];
}
}
- 时间复杂度:求最短路的复杂度为 $O(m\log{n})$,DP 过程坏情况下要扫完所有的边,复杂度为 $O(m)$。整体复杂度为 $O(m\log{n})$
- 空间复杂度:$O(n + m)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.1786 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
