LC 477. 汉明距离总和

题目描述

这是 LeetCode 上的 477. 汉明距离总和 ，难度为 中等。

两个整数的汉明距离指的是这两个数字的二进制数对应位不同的数量。

给你一个整数数组 nums，请你计算并返回 nums 中任意两个数之间汉明距离的总和。

示例 1：

1
2
3
4
5
6
7
输入：nums = [4,14,2]

输出：6

解释：在二进制表示中，4 表示为 0100 ，14 表示为 1110 ，2表示为 0010 。（这样表示是为了体现后四位之间关系）
所以答案为：
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6

示例 2：
1
2
3
输入：nums = [4,14,4]

输出：4

提示：

  • $1 <= nums.length <= 10^5$
  • $0 <= nums[i] <= 10^9$
  • 给定输入的对应答案符合 32-bit 整数范围

按位统计

我们知道，汉明距离为两数二进制表示中不同位的个数，同时每位的统计是相互独立的。

即最终的答案为 $\sum_{x = 0}^{31} calc(x)$，其中 $calc$ 函数为求得所有数二进制表示中的某一位 $x$ 所产生的不同位的个数。

我们考虑某个 $cacl(x)$ 如何求得：

事实上，对于某个 nums[i] 我们只关心在 nums 中有多少数的第 $x$ 位的与其不同，而不关心具体是哪些数与其不同，同时二进制表示中非 $0$ 即 $1$。

这指导我们可以建立两个集合 $s0$ 和 $s1$，分别统计出 nums 中所有数的第 $x$ 位中 $0$ 的个数和 $1$ 的个数，集合中的每次计数代表了 nums 中的某一元素，根据所在集合的不同代表了其第 $x$ 位的值。那么要找到在 nums 中有多少数与某一个数的第 $x$ 位不同，只需要读取另外一个集合的元素个数即可，变成了 $O(1)$ 操作。那么要求得「第 $x$ 位所有不同数」的对数的个数，只需要应用乘法原理，将两者元素个数相乘即可。

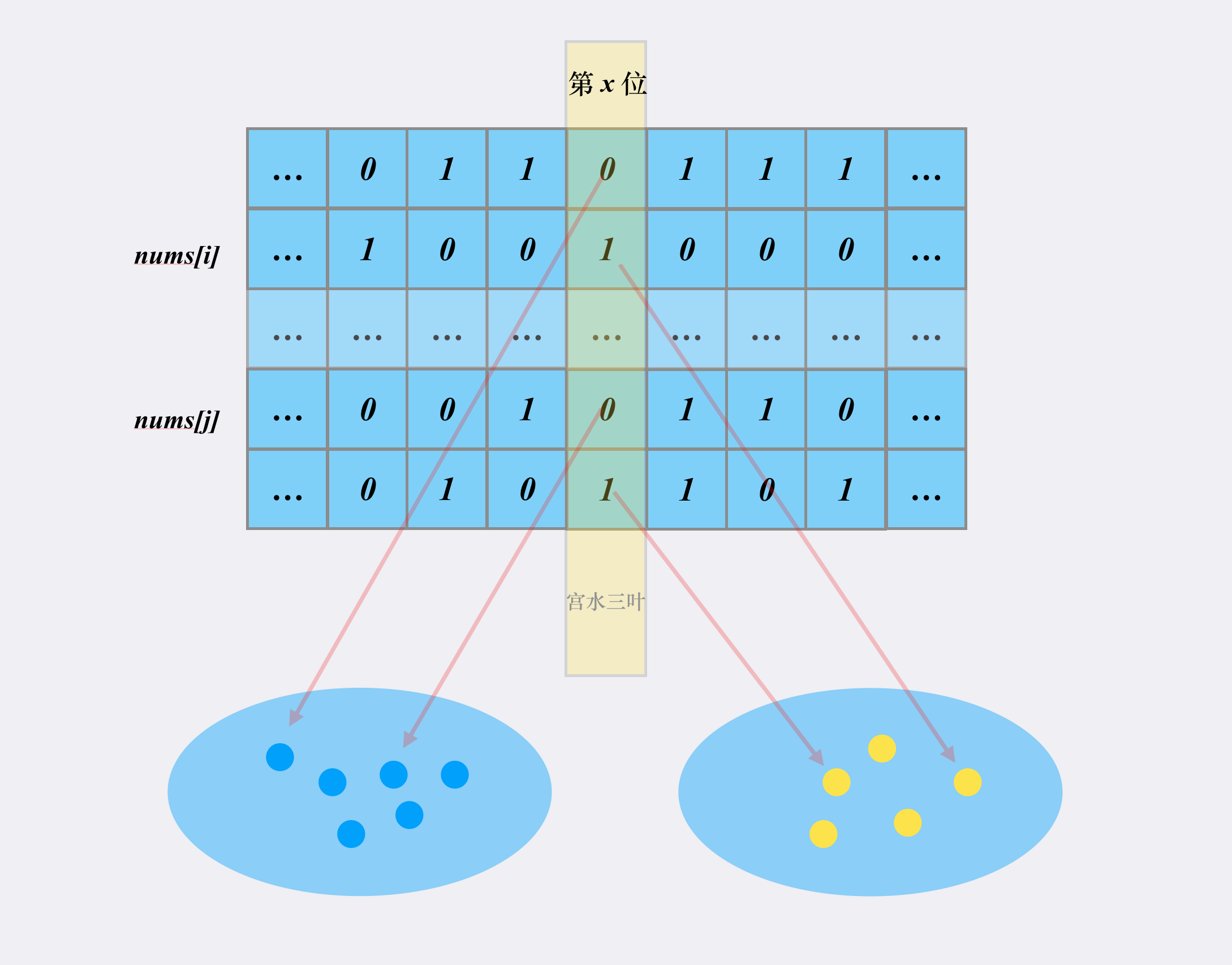
前面说到每位的统计是相对独立的，因此只要对「每一位」都应用上述操作，并把「每一位」的结果累加即是最终答案。

Java 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int totalHammingDistance(int[] nums) {
        int ans = 0;
        for (int x = 31; x >= 0; x--) {
            int s0 = 0, s1 = 0;
            for (int u : nums) {
                if (((u >> x) & 1) == 1) s1++;    
                else s0++;
            }
            ans += s0 * s1;
        }
        return ans;
    }
}

C++ 代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int totalHammingDistance(vector<int>& nums) {
        int ans = 0;
        for (int x = 31; x >= 0; x--) {
            int s0 = 0, s1 = 0;
            for (int u : nums) {
                if (((u >> x) & 1) == 1) s1++;
                else s0++;
            }
            ans += s0 * s1;
        }
        return ans;
    }
};

Python 代码：
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def totalHammingDistance(self, nums: List[int]) -> int:
        ans = 0
        for x in range(31, -1, -1):
            s0, s1 = 0, 0
            for u in nums:
                if ((u >> x) & 1) == 1:
                    s1 += 1
                else:
                    s0 += 1
            ans += s0 * s1
        return ans

TypeScript 代码：
1
2
3
4
5
6
7
8
9
10
11
12
function totalHammingDistance(nums: number[]): number {
    let ans = 0;
    for (let x = 31; x >= 0; x--) {
        let s0 = 0, s1 = 0;
        for (let u of nums) {
            if (((u >> x) & 1) == 1) s1++;
            else s0++;
        }
        ans += s0 * s1;
    }
    return ans;
};

  • 时间复杂度：$O(C \times n)$，$C$ 固定为 $32$
  • 空间复杂度：$O(1)$

最后

这是我们「刷穿 LeetCode」系列文章的第 No.477 篇，系列开始于 2021/01/01，截止于起始日 LeetCode 上共有 1916 道题目，部分是有锁题，我们将先把所有不带锁的题目刷完。

在这个系列文章里面，除了讲解解题思路以外，还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。

为了方便各位同学能够电脑上进行调试和提交代码，我建立了相关的仓库：https://github.com/SharingSource/LogicStack-LeetCode 。

在仓库地址里，你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。