LC 787. K 站中转内最便宜的航班
题目描述
这是 LeetCode 上的 787. K 站中转内最便宜的航班 ,难度为 中等。
有 n 个城市通过一些航班连接。给你一个数组 flights,其中 $flights[i] = [from_i, to_i, price_i]$ ,表示该航班都从城市 $from_i$ 开始,以价格 $price_i$ 抵达 $to_i$。
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
示例 1:1
2
3
4
5
6
7
8
9输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释:
城市航班图如下
从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。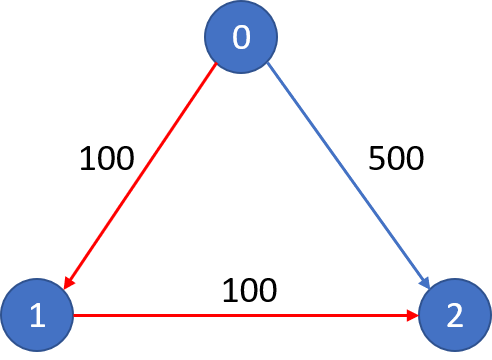
示例 2:1
2
3
4
5
6
7
8
9输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出: 500
解释:
城市航班图如下
从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,如图中蓝色所示。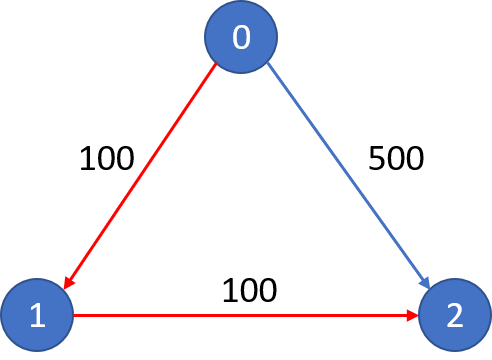
提示:
- 1 <= n <= 100
- 0 <= flights.length <= (n * (n - 1) / 2)
- flights[i].length == 3
- 0 <= fromi, toi < n
- fromi != toi
- 1 <= pricei <= $10^4$
- 航班没有重复,且不存在自环
- 0 <= src, dst, k < n
- src != dst
基本分析
从题面看就能知道,这是一类「有限制」的最短路问题。
「限制最多经过不超过 $k$ 个点」等价于「限制最多不超过 $k + 1$ 条边」,而解决「有边数限制的最短路问题」是 SPFA 所不能取代 Bellman Ford 算法的经典应用之一(SPFA 能做,但不能直接做)。
Bellman Ford/SPFA 都是基于动态规划,其原始的状态定义为 $f[i][k]$ 代表从起点到 $i$ 点,且经过最多 $k$ 条边的最短路径。这样的状态定义引导我们能够使用 Bellman Ford 来解决有边数限制的最短路问题。
同样多源汇最短路算法 Floyd 也是基于动态规划,其原始的三维状态定义为 $f[i][j][k]$ 代表从点 $i$ 到点 $j$,且经过的所有点编号不会超过 $k$(即可使用点编号范围为 $[1, k]$)的最短路径。这样的状态定义引导我们能够使用 Floyd 求最小环或者求“重心点”(即删除该点后,最短路值会变大)。
如果你对几类最短算法不熟悉,可以看 这里,里面涵盖所有的「最短路算法」和「存图方式」。
Bellman Ford + 邻接矩阵
回到本题,「限制最多经过不超过 $k$ 个点」等价于「限制最多不超过 $k + 1$ 条边」,因此可以使用 Bellman Ford 来求解。
点的数量只有 $100$,可以直接使用「邻接矩阵」的方式进行存图。
需要注意的是,在遍历所有的“点对/边”进行松弛操作前,需要先对 $dist$ 进行备份,否则会出现「本次松弛操作所使用到的边,也是在同一次迭代所更新的」,从而不满足边数限制的要求。
举个 🌰,例如本次松弛操作使用了从 $a$ 到 $b$ 的当前最短距离来更新 $dist[b]$,直接使用 $dist[a]$ 的话,不能确保 $dist[a]$ 不是在同一次迭代中所更新,如果 $dist[a]$ 是同一次迭代所更新的话,那么使用的边数将会大于 $k$ 条。
因此在每次迭代开始前,我们都应该对 $dist$ 进行备份,在迭代时使用备份来进行松弛操作。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
int N = 110, INF = 0x3f3f3f3f;
int[][] g = new int[N][N];
int[] dist = new int[N];
int n, m, s, t, k;
public int findCheapestPrice(int _n, int[][] flights, int _src, int _dst, int _k) {
n = _n; s = _src; t = _dst; k = _k + 1;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
g[i][j] = i == j ? 0 : INF;
}
}
for (int[] f : flights) {
g[f[0]][f[1]] = f[2];
}
int ans = bf();
return ans > INF / 2 ? -1 : ans;
}
int bf() {
Arrays.fill(dist, INF);
dist[s] = 0;
for (int limit = 0; limit < k; limit++) {
int[] clone = dist.clone();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dist[j] = Math.min(dist[j], clone[i] + g[i][j]);
}
}
}
return dist[t];
}
}
- 时间复杂度:$O(k * n^2)$
- 空间复杂度:$O(n^2)$
Bellman Ford + 类
我们知道 Bellman Ford 需要遍历所有的边,而使用「邻接矩阵」的存图方式让我们不得不遍历所有的点对,复杂度为 $O(n^2)$。
而边的数量 $m$ 的数据范围为 $0 <= flights.length <= (n * (n - 1) / 2)$,因此我们可以使用「类」的方式进行存图,从而确保在遍历所有边的时候,复杂度严格为 $O(m)$,而不是 $O(n^2)$。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33class Solution {
class Edge {
int x, y, w;
Edge(int _x, int _y, int _w) {
x = _x; y = _y; w = _w;
}
}
int N = 110, INF = 0x3f3f3f3f;
int[] dist = new int[N];
List<Edge> list = new ArrayList<>();
int n, m, s, t, k;
public int findCheapestPrice(int _n, int[][] flights, int _src, int _dst, int _k) {
n = _n; s = _src; t = _dst; k = _k + 1;
for (int[] f : flights) {
list.add(new Edge(f[0], f[1], f[2]));
}
m = list.size();
int ans = bf();
return ans > INF / 2 ? -1 : ans;
}
int bf() {
Arrays.fill(dist, INF);
dist[s] = 0;
for (int i = 0; i < k; i++) {
int[] clone = dist.clone();
for (Edge e : list) {
int x = e.x, y = e.y, w = e.w;
dist[y] = Math.min(dist[y], clone[x] + w);
}
}
return dist[t];
}
}
- 时间复杂度:共进行 $k + 1$ 次迭代,每次迭代备份数组复杂度为 $O(n)$,然后遍历所有的边进行松弛操作,复杂度为 $O(m)$。整体复杂度为 $O(k * (n + m))$
- 空间复杂度:$O(n + m)$
Bellman Ford
更进一步,由于 Bellman Ford 核心操作需要遍历所有的边,因此也可以直接使用 $flights$ 数组作为存图信息,而无须额外存图。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
int N = 110, INF = 0x3f3f3f3f;
int[] dist = new int[N];
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
Arrays.fill(dist, INF);
dist[src] = 0;
for (int limit = 0; limit < k + 1; limit++) {
int[] clone = dist.clone();
for (int[] f : flights) {
int x = f[0], y = f[1], w = f[2];
dist[y] = Math.min(dist[y], clone[x] + w);
}
}
return dist[dst] > INF / 2 ? -1 : dist[dst];
}
}
- 时间复杂度:共进行 $k + 1$ 次迭代,每次迭代备份数组复杂度为 $O(n)$,然后遍历所有的边进行松弛操作,复杂度为 $O(m)$。整体复杂度为 $O(k * (n + m))$
- 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.787 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
