LC 675. 为高尔夫比赛砍树
题目描述
这是 LeetCode 上的 675. 为高尔夫比赛砍树 ,难度为 困难。
你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 $m \times n$ 的矩阵表示, 在这个矩阵中:
- $0$ 表示障碍,无法触碰
- $1$ 表示地面,可以行走
- 比 $1$ 大的数 表示有树的单元格,可以行走,数值表示树的高度
每一步,你都可以向上、下、左、右四个方向之一移动一个单位,如果你站的地方有一棵树,那么你可以决定是否要砍倒它。
你需要按照树的高度从低向高砍掉所有的树,每砍过一颗树,该单元格的值变为 $1$(即变为地面)。
你将从 $(0, 0)$ 点开始工作,返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树,返回 $-1$ 。
可以保证的是,没有两棵树的高度是相同的,并且你至少需要砍倒一棵树。
示例 1: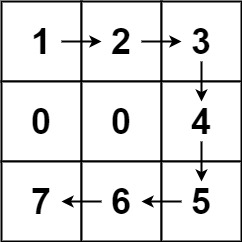
1
2
3
4
5输入:forest = [[1,2,3],[0,0,4],[7,6,5]]
输出:6
解释:沿着上面的路径,你可以用 6 步,按从最矮到最高的顺序砍掉这些树。
示例 2: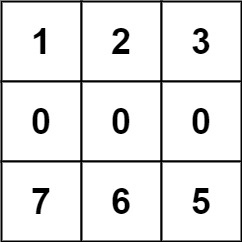
1
2
3
4
5输入:forest = [[1,2,3],[0,0,0],[7,6,5]]
输出:-1
解释:由于中间一行被障碍阻塞,无法访问最下面一行中的树。
示例 3:1
2
3
4
5
6输入:forest = [[2,3,4],[0,0,5],[8,7,6]]
输出:6
解释:可以按与示例 1 相同的路径来砍掉所有的树。
(0,0) 位置的树,可以直接砍去,不用算步数。
提示:
- $m == forest.length$
- $n == forest[i].length$
- $1 <= m, n <= 50$
- $0 <= forest[i][j] <= 10^9$
基本分析
基本题意为:给定一个 $n \times m$ 的矩阵,每次能够在当前位置往「四联通」移动一个单位,其中 $0$ 的位置代表障碍(无法访问),$1$ 的位置代表平地(可直接访问,且无须进行任何决策),其余大于 $1$ 的位置代表有树,经过该位置的时候可以考虑将树砍掉(相应值变为平地 $1$)。
同时题目限定了我们只能按照「从低到高」的顺序进行砍树,并且图中不存在高度相等的两棵树,这意味着 整个砍树的顺序唯一确定,就是对所有有树的地方进行「高度」排升序,即是完整的砍树路线。
而另外一个更为重要的性质是:点与点之间的最短路径,不会随着砍树过程的进行而发生变化(某个树点被砍掉,只会变为平地,不会变为阻碍点,仍可通过)。
综上,砍树的路线唯一确定,当我们求出每两个相邻的砍树点最短路径,并进行累加即是答案(整条砍树路径的最少步数)。
BFS
因此,再结合数据范围只有 $50$,并且点与点之间边权为 $1$(每次移动算一步),我们可以直接进行 BFS 进行求解。
先对整张图进行一次遍历,预处理出所有的树点(以三元组 $(height, x, y)$ 的形式进行存储),并对其以 $height$ 排升序,得到唯一确定的砍树路径。
之后就是计算砍树路径中相邻点的最短距离,运用 BFS 求解任意两点的最短路径复杂度为 $O(n \times m)$,我们最多有 $n \times m$ 个树点,因此整体复杂度为 $O(n^2 * \times m^2)$。
求解相邻点的最短距离的部分也是整个算法的复杂度上界,数据范围只有 $50$,计算量不超过 $10^7$,可以过。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52class Solution {
int N = 50;
int[][] g = new int[N][N];
int n, m;
List<int[]> list = new ArrayList<>();
public int cutOffTree(List<List<Integer>> forest) {
n = forest.size(); m = forest.get(0).size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
g[i][j] = forest.get(i).get(j);
if (g[i][j] > 1) list.add(new int[]{g[i][j], i, j});
}
}
Collections.sort(list, (a,b)->a[0]-b[0]);
if (g[0][0] == 0) return -1;
int x = 0, y = 0, ans = 0;
for (int[] ne : list) {
int nx = ne[1], ny = ne[2];
int d = bfs(x, y, nx, ny);
if (d == -1) return -1;
ans += d;
x = nx; y = ny;
}
return ans;
}
int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
int bfs(int X, int Y, int P, int Q) {
if (X == P && Y == Q) return 0;
boolean[][] vis = new boolean[n][m];
Deque<int[]> d = new ArrayDeque<>();
d.addLast(new int[]{X, Y});
vis[X][Y] = true;
int ans = 0;
while (!d.isEmpty()) {
int size = d.size();
while (size-- > 0) {
int[] info = d.pollFirst();
int x = info[0], y = info[1];
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (g[nx][ny] == 0 || vis[nx][ny]) continue;
if (nx == P && ny == Q) return ans + 1;
d.addLast(new int[]{nx, ny});
vis[nx][ny] = true;
}
}
ans++;
}
return -1;
}
}
- 时间复杂度:预处理出所有树点的复杂度为 $O(n \times m)$,对树点进行排序的复杂度为 $O(nm \log{nm})$,最多有 $n \times m$ 个树点,对每两个相邻树点运用
BFS求最短路的复杂度为 $O(n \times m)$,统计完整路径的复杂度为 $O(n^2 \times m^2)$ - 空间复杂度:$O(n \times m)$
AStar 算法
由于问题的本质是求最短路,同时原问题的边权为 $1$,因此套用其他复杂度比 BFS 高的最短路算法,对于本题而言是没有意义,但运用启发式搜索 AStar 算法来优化则是有意义。
因为在 BFS 过程中,我们会无差别往「四联通」方向进行搜索,直到找到「当前树点的下一个目标位置」为止,而实际上,两点之间的最短路径往往与两点之间的相对位置相关。
举个 🌰,当前我们在位置 $S$,我们目标位置是 $T$,而 $T$ 在 $S$ 的右下方,此时我们应当优先搜索方向”往右下方”的路径,当无法从”往右下方”的路径到达 $T$,我们再考虑搜索其他大方向的路径:
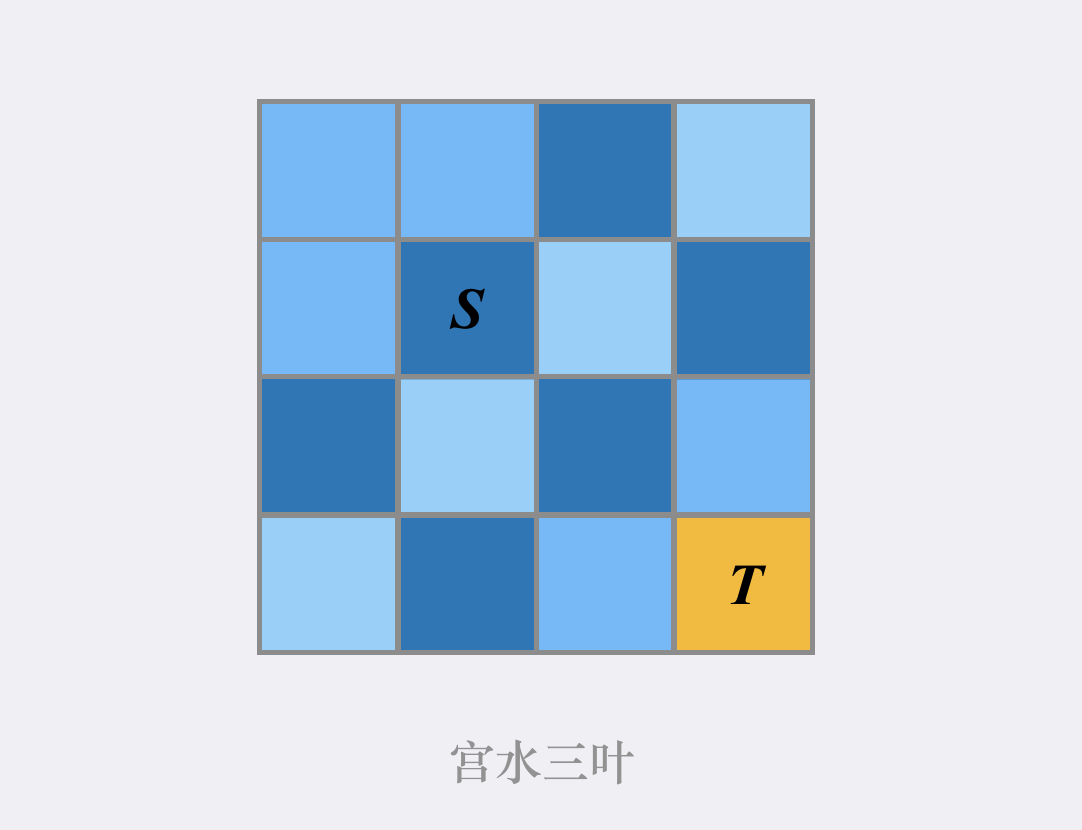
如何设计这样带有优先级的搜索顺序,则是 AStar 算法「启发式函数」的设计过程,其本质是对应了对「最小步数」的估算,只有当我们确保「最小步数估算 $\leq $ 实际最小步数」,AStar 算法的正确性才得以保证。
因此我们往往会直接使用「理论最小步数」来作为启发式函数的,对于本题,可直接使用「曼哈顿距离」作为「理论最小步数」。
因此,如果我们是要从源点 $S$ 到汇点 $T$,并且当前位于中途点 $x$ 的话,点 $x$ 的最小步数估算包括两部分:到点 $x$ 的实际步数 + 从点 $x$ 到点 $T$ 的理论最小步数(曼哈顿距离)。使用「优先队列」按照「总的最小步数估算」进行出队,即可实现 AStar 算法的搜索顺序。
AStar 算法做过很多次了,相关合集可以在 这里 看到。
另外,网上很多对 AStar 正确性证明不了解的人,会缺少以下map.get(nidx) > step + 1判断逻辑。
简单来说,启发式函数的设计是针对汇点而言的,因此 AStar 算法搜索过程只确保对 $T$ 的出入队次序能够对应回到点 $T$ 第 $k$ 短路,而对于其余点的出入队次序到其余点的最短路没有必然的对应关系,因此当某个点的最小步数被更新,我们是要将其进行再次入队的。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55class Solution {
int N = 50;
int[][] g = new int[N][N];
int n, m;
List<int[]> list = new ArrayList<>();
public int cutOffTree(List<List<Integer>> forest) {
n = forest.size(); m = forest.get(0).size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
g[i][j] = forest.get(i).get(j);
if (g[i][j] > 1) list.add(new int[]{g[i][j], i, j});
}
}
if (g[0][0] == 0) return -1;
Collections.sort(list, (a,b)->a[0]-b[0]);
int x = 0, y = 0, ans = 0;
for (int[] ne : list) {
int nx = ne[1], ny = ne[2];
int d = astar(x, y, nx, ny);
if (d == -1) return -1;
ans += d;
x = nx; y = ny;
}
return ans;
}
int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
int getIdx(int x, int y) {
return x * m + y;
}
int f(int X, int Y, int P, int Q) {
return Math.abs(X - P) + Math.abs(Y - Q);
}
int astar(int X, int Y, int P, int Q) {
if (X == P && Y == Q) return 0;
Map<Integer, Integer> map = new HashMap<>();
PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[0]-b[0]);
q.add(new int[]{f(X, Y, P, Q), X, Y});
map.put(getIdx(X, Y), 0);
while (!q.isEmpty()) {
int[] info = q.poll();
int x = info[1], y = info[2], step = map.get(getIdx(x, y));
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1], nidx = getIdx(nx, ny);
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (g[nx][ny] == 0) continue;
if (nx == P && ny == Q) return step + 1;
if (!map.containsKey(nidx) || map.get(nidx) > step + 1) {
q.add(new int[]{step + 1 + f(nx, ny, P, Q), nx, ny});
map.put(nidx, step + 1);
}
}
}
return -1;
}
}
- 时间复杂度:启发式搜索分析时空复杂度意义不大
- 空间复杂度:启发式搜索分析时空复杂度意义不大
AStar 算法 + 并查集预处理无解
我们知道,AStar 算法使用到了「优先队列(堆)」来进行启发式搜索,而对于一些最佳路径方向与两点相对位置相反(例如 $T$ 在 $S$ 的右边,但由于存在障碍,最短路径需要先从左边绕一圈才能到 $T$),AStar 反而会因为优先队列(堆)而多一个 $\log$ 的复杂度。
因此一个可行的优化是,我们先提前处理「无解」的情况,常见的做法是在预处理过程中运用「并查集」来维护连通性。
这种对于不影响复杂度上界的预处理相比后续可能出现的大量无效搜索(最终无解)的计算量而言,是有益的。
代码:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80class Solution {
int N = 50;
int[][] g = new int[N][N];
int n, m;
int[] p = new int[N * N + 10];
List<int[]> list = new ArrayList<>();
void union(int a, int b) {
p[find(a)] = p[find(b)];
}
boolean query(int a, int b) {
return find(a) == find(b);
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int getIdx(int x, int y) {
return x * m + y;
}
public int cutOffTree(List<List<Integer>> forest) {
n = forest.size(); m = forest.get(0).size();
// 预处理过程中,同时使用「并查集」维护连通性
for (int i = 0; i < n * m; i++) p[i] = i;
int[][] tempDirs = new int[][]{{0,-1},{-1,0}};
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
g[i][j] = forest.get(i).get(j);
if (g[i][j] > 1) list.add(new int[]{g[i][j], i, j});
if (g[i][j] == 0) continue;
// 只与左方和上方的区域联通即可确保不重不漏
for (int[] di : tempDirs) {
int nx = i + di[0], ny = j + di[1];
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (g[nx][ny] != 0) union(getIdx(i, j), getIdx(nx, ny));
}
}
}
// 若不满足所有树点均与 (0,0),提前返回无解
for (int[] info : list) {
int x = info[1], y = info[2];
if (!query(getIdx(0, 0), getIdx(x, y))) return -1;
}
Collections.sort(list, (a,b)->a[0]-b[0]);
int x = 0, y = 0, ans = 0;
for (int[] ne : list) {
int nx = ne[1], ny = ne[2];
int d = astar(x, y, nx, ny);
if (d == -1) return -1;
ans += d;
x = nx; y = ny;
}
return ans;
}
int f(int X, int Y, int P, int Q) {
return Math.abs(X - P) + Math.abs(Y - Q);
}
int[][] dirs = new int[][]{{0,1},{0,-1},{1,0},{-1,0}};
int astar(int X, int Y, int P, int Q) {
if (X == P && Y == Q) return 0;
Map<Integer, Integer> map = new HashMap<>();
PriorityQueue<int[]> q = new PriorityQueue<>((a,b)->a[0]-b[0]);
q.add(new int[]{f(X, Y, P, Q), X, Y});
map.put(getIdx(X, Y), 0);
while (!q.isEmpty()) {
int[] info = q.poll();
int x = info[1], y = info[2], step = map.get(getIdx(x, y));
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1], nidx = getIdx(nx, ny);
if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
if (g[nx][ny] == 0) continue;
if (nx == P && ny == Q) return step + 1;
if (!map.containsKey(nidx) || map.get(nidx) > step + 1) {
q.add(new int[]{step + 1 + f(nx, ny, P, Q), nx, ny});
map.put(nidx, step + 1);
}
}
}
return -1;
}
}
- 时间复杂度:启发式搜索分析时空复杂度意义不大
- 空间复杂度:启发式搜索分析时空复杂度意义不大
最后
这是我们「刷穿 LeetCode」系列文章的第 No.675 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!
